RESEARCH
Upper Bounding Unit Distance Graphs
Keywords: beam search; unit distance graphs; exploitation-exploration; planar geometry; combinatorial optimization
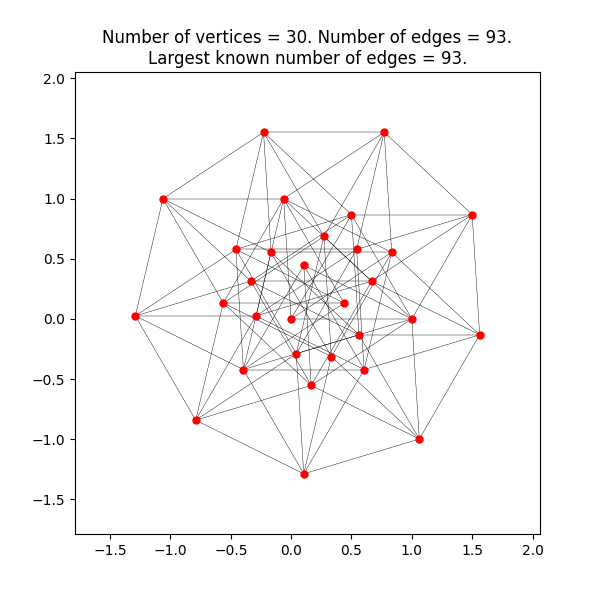
What is the maximum number of edges u(n) that a unit distance graph (UDG) of n vertices can have, as asked by an unsolved problem of Paul Erdős? We address the problem of determining the maximum number of edges in a UDG of n vertices using computer search. We seek to demonstrate a computer algorithm to generate dense UDGs for vertex counts up to at least 100. Via beam search with an added visitation metric, our algorithm finds all known maximally dense UDGs up to isomorphism at the push of a button. In addition, for 15 < n, where u(n) is unknown, i) the algorithm finds all previously published densest UDGs up to isomorphism for 15 < n ≤ 30, ii) the rate of growth of u(n)/n remains similar for 30 < n. iii) we build a database of over 60 million UDGs found by our algorithm. The preprint of the paper is available on arXiv.
★Features:
- Designed a novel heuristic beam search algorithm to improved the maximum number of edges in unit distance graphs.
- Explored graph constructions from the Moser Lattice with heuristic generating rules like rotation, translation, and reflection.
- Used multiprocessor and GPU implementations to optimize the efficiency of the search algorithms.
★Skills: Python; Numpy, Matplotlib, Pandas, Scikit-learn, Multiprocessing.
Laplacian Eigenmaps and Chebyshev Polynomials
Subjects: probability; metric geometry; statistics theory
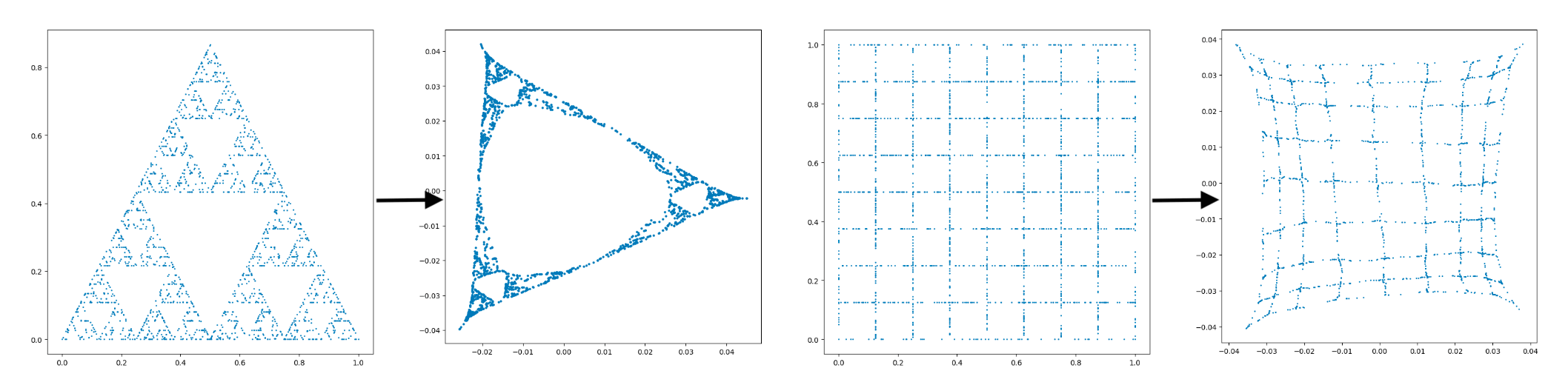
Eigenmaps are important in analysis, geometry, and machine learning, particularly in nonlinear dimension reduction. This project investigates the relationship between eigen-coordinates of graph Laplacians and Chebyshev polynomials. We will consider constructing graph Laplacian operators on $[-1,1]$, $[-1,1]^2$, the sphere $S^2$, and the Sierpinski gasket. We also have explored these operators when the points are selected randomly with various distributions, such as uniform and Gaussian. We have developed algorithms capable of generating eigenmap plots for the aforementioned sample spaces. In our next step, we would also like to compare the eigen-coordinates of graph Laplacian operators constructed from those intervals with families of orthogonal polynomials, such as the Hermite polynomials and possibly exceptional orthogonal polynomials. The paper is available on the UConn REU website.
★Features:
- Studied eigenmaps of Laplacian matrices transforming high-dimensional data into graph representations.
- Use NumPy and Matplotlib to visualize the eigenmaps.
- Explored the properties of eigenmaps, including data distribution, manifold smoothness, and boundary conditions.
- Analyzed eigenmaps on structures including intervals, squares, torus, and the Sierpinski triangle, emphasizing their connections to orthogonal polynomials and optimal parameter choices.
★Skills: Python, MATLAB; NumPy.
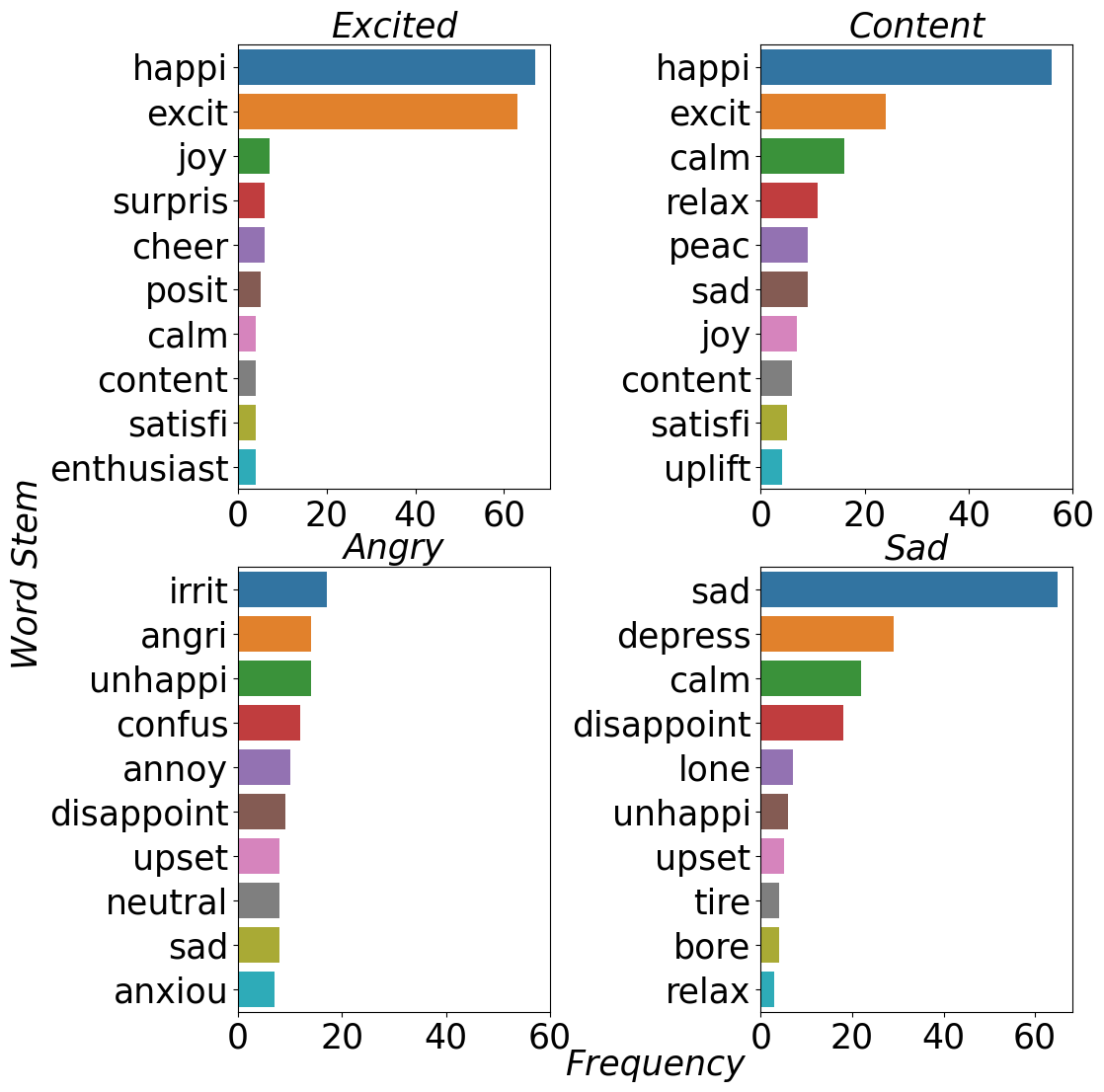
Dimensional Design of Emotive Sounds for Robots
HRI '24: Proceedings of the 2024 ACM/IEEE International Conference on Human-Robot Interaction
Keywords: non-linguistic utterances; human-robot interaction; emotive sound; algorithmic composition
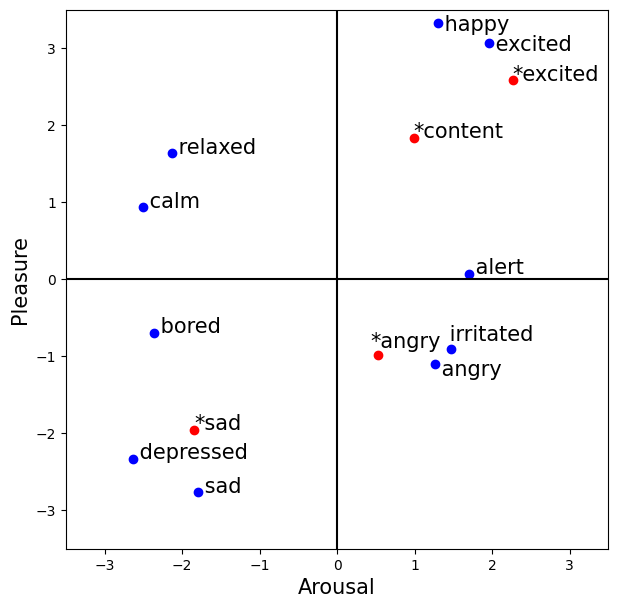
Non-Linguistic Utterances (NLUs) are crucial in both human-human and human-robot interactions. We explored how specific audio qualities affect the perception of emotional arousal and pleasure. A novel generative algorithm was designed to express various emotions using musical and prosodic parameters. An end-user evaluation had participants interpret NLUs representing excitement, contentment, sadness, and anger. The study revealed that participants consistently associated excited, sad and angry NLUs with significantly different emotional states but not for content NLUs. Results are published in the 2024 ACM/IEEE International Conference on Human-Robot Interaction (HRI '24).
★Features:
- Implemented a non-linguistic utterances generator conveying emotions on the DARwIn-OP robot.
- Designed motions for the robot and developed the user study.
- Conducted user studies to explore the perception of non-linguistic utterances generated by the robot.
- Analyzed experimental data to explore the correlation between non-linguistic utterances and emotions.
★Skills: Python, C++; Numpy, Matplotlib, Pandas, Scikit-learn, nltk, statsmodels, seaborn.
SELECTED PROJECTS
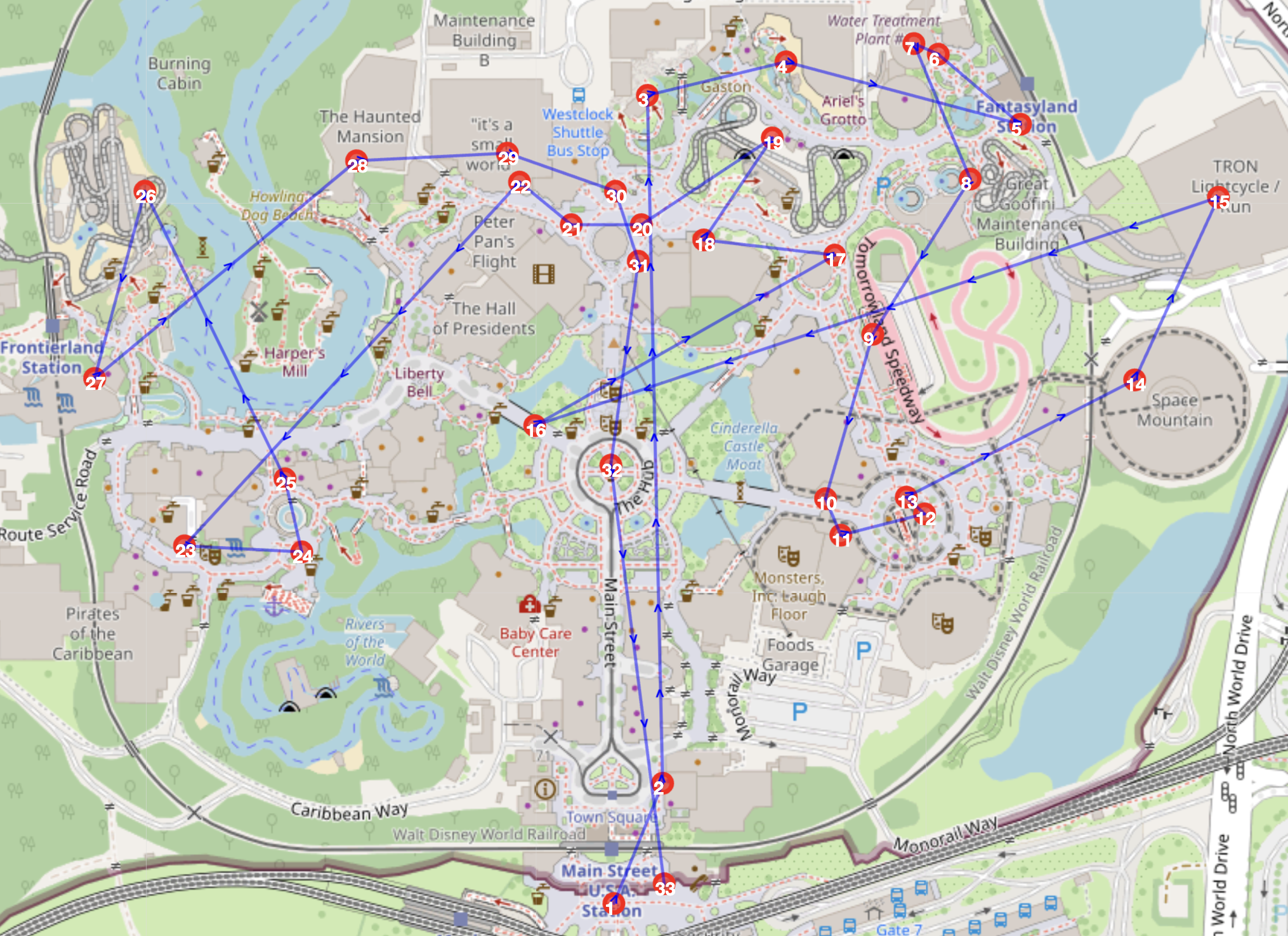
Optimizing a One-Day Disneyland Itinerary
This project tackles the challenge of making the most of a one-day visit to Disneyland Magic Kingdom. Using real wait time data, park layout, and integer programming, it generates optimal schedules to maximize rides played, minimize wait and walking time, and balance personal preferences. Inspired by the Traveling Salesman Problem (TSP), the model produces itineraries that adapt to park conditions and visitor priorities, offering a smarter and more enjoyable park experience.
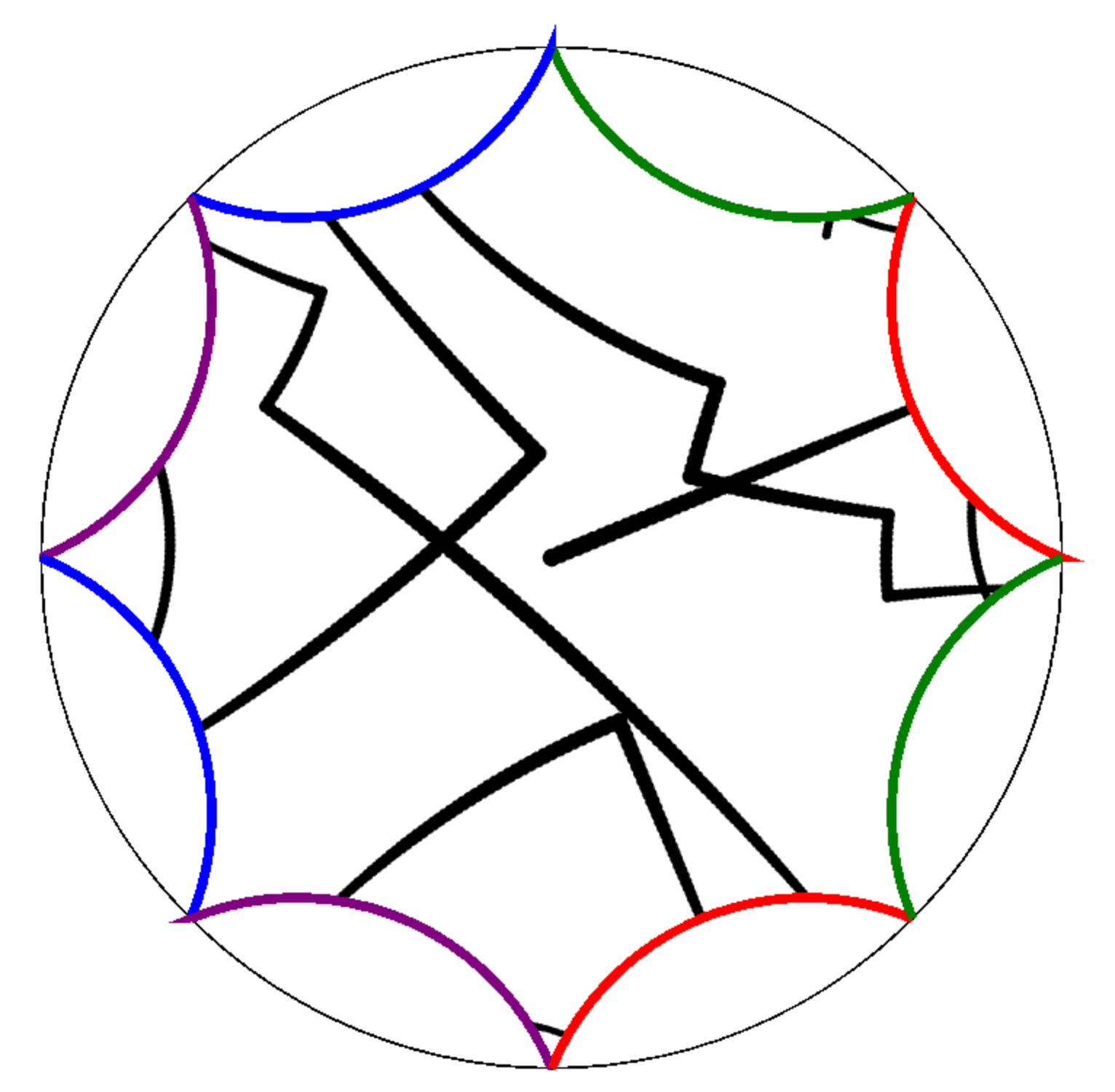
Computer Visualizations on the Hyperbolic Plane
This project explores games and visualizations designed in hyperbolic geometry, inspired by the game HyperRogue, which takes place in the Poincaré disk model of the hyperbolic plane. Fascinated by the geometry and mechanics, I researched other non-Euclidean games like Hyperbolica and Hypermine, and eventually created my own interactive visualizations using the Hyperbolic Canvas JavaScript library. This project combines mathematical understanding with basic web programming to simulate geodesics and tilings in hyperbolic space.
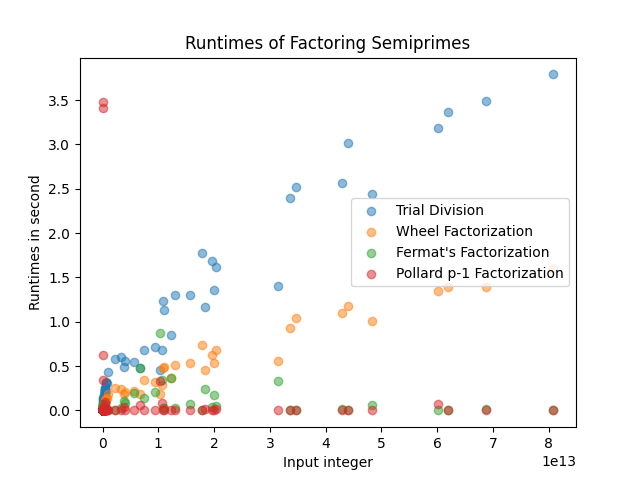
Integer Factorization Algorithms
This project investigates the problem of decomposing composite numbers into prime factors, a fundamental question in number theory and cryptography. I implemented and compared five classical algorithms—Trial Division, Wheel Factorization, Fermat's Method, Kraitchik-Fermat, and Pollard's p − 1—evaluating their runtime across different inputs. Through this exploration, I gained insight into the computational complexity of integer factorization and how algorithmic improvements affect performance in practice.